回溯法解决的问题

回溯法，一般可以解决如下几种问题：

  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 棋盘问题：N皇后，解数独等等

组合是不强调元素顺序的，排列是强调元素顺序。

例如：{1, 2} 和 {2, 1} 在组合上，就是一个集合，因为不强调顺序，而要是排列的话，{1, 2} 和 {2, 1} 就是两个集合了。

回溯模板

1
2
3
4
5
6
7
8
9
10
11
12
void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}
  • 回溯搜索的遍历过程

回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度。

如图：回溯算法示意图

  • 关于递归传参startIndex问题

    同个集合来求组合的话，就需要startIndex；多个集合取组合，各个集合之间相互不影响，那么就不用startIndex

    • 一个集合中的元素不能重复选取类型（递归参数需要传入startIndex，表示下一轮递归遍历的起始位置）

      每次从集合中选取元素，可选择的范围随着选择的进行而收缩，调整可选择的范围，就是要靠startIndex递归的参数

    • 多个集合中的元素不能重复选取类型。（不需要startIndex）

    • 一个集合中的元素可以无限重复选取，但是有总和的限制。（横向遍历不能重复取，需要startIndex，但是纵向遍历可以重复读取当前的数，所以递归的时候传参i）

    • 一个集合中的元素只能使用一次，并且数组是有重复的元。（需要startIndex，并且要先排序数组，然后进行剪枝）

  • 剪枝精髓是：for循环在寻找起点的时候要有一个范围，如果这个起点到集合终止之间的元素已经不够 题目要求的k个元素了，就没有必要搜索了。

  • 在求和问题中，排序之后加剪枝是常见的套路！

  • 关于去重问题

    回溯算法：递增子序列的去重是同一个父节点下的本层的去重。

    回溯算法：求子集问题（二）的去重是要整颗树的本层去重，但是整棵树的同一层去重不好操作，所以才排序，与前一个树枝对比就可以了。

组合问题

一个集合中的元素不能重复选取类型（递归参数需要传入startIndex，表示下一轮递归遍历的起始位置）

组合

Leetcode：77.组合

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

思路：递归来做层叠嵌套（可以理解是写k层for循环），每一次的递归中嵌套一个for循环，那么递归就可以用于解决多层嵌套循环的问题了。

回溯算法组合问题示意图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
var ( 
    path []int
    result [][]int
)

func combine(n int, k int) [][]int {
    path, result = make([]int, 0, k), make([][]int, 0)
    backtracking(n, k, 1)   // 因为n从1开始，索引startIndex传1
    return result
}

func backtracking(n, k, startIndex int) {
    if len(path) == k {
        tmp := make([]int, k)   // path需要重复使用，go中要拷贝一份
        copy(tmp, path)
        result = append(result, tmp)
        return
    }

    for i := startIndex; i <= n; i++ {  // 横向遍历，从startIndex开始，不往回走，避免出现重复组合
        if n - i + len(path) + 1 < k {  // 剪枝
            break
        }
        path = append(path, i)      // 处理
        backtracking(n, k, i+1)     // 递归，纵向遍历，已经取过i了，所以下一层从i+1开始往后取数
        path = path[:len(path)-1]   // 回溯，撤销处理的节点
    }
}
  • 时间复杂度: O(n * 2^n)
  • 空间复杂度: O(n)

组合总和III

Leetcode：216.组合总和III

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

  • 所有数字都是正整数。
  • 解集不能包含重复的组合。

示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]

示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
var (
    path []int
    res [][]int
)

func combinationSum3(k int, n int) [][]int {
    path, res = make([]int, 0, k), make([][]int, 0)
    backtracking(n, k, 0, 1)
    return res
}

// 一个集合中的元素不能重复选取类型（递归参数需要传入startIndex，表示下一轮递归遍历的起始位置）
func backtracking(n, k, sum, startIndex int) {
    if sum == n && len(path) == k {		// 两个条件，总和 和 个数
        tmp := make([]int, len(path))
        copy(tmp, path)
        res = append(res, tmp)
        return
    }

    for i := startIndex; i <= 9; i++ {
        if 9 - i + len(path) + 1 < k || sum + i > n {	// 剪枝
            break
        }
        path = append(path, i)
        sum += i
        backtracking(n, k, sum, i+1)
        path = path[:len(path)-1]   // 回溯
        sum -= i                    // 回溯
    }
}
  • 时间复杂度: O(n * 2^n)
  • 空间复杂度: O(n)

多个集合中的元素不能重复选取类型。（不需要startIndex）

电话号码的字母组合

Leetcode：17.电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射与电话按键相同。注意 1 不对应任何字母。

示例:

  • 输入：”23”
  • 输出：[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].

说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

思路：因为本题每一个数字代表的是不同集合，也就是求不同集合之间的组合，与之前在同一个集合中的求组合不同。所以注意这里for循环是从0开始的，并不是从startIndex的；当前中的index代表digits中的第几个数字。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
var (
    m []string
    path []byte
    res []string
)

func letterCombinations(digits string) []string {
    // 前两个分别代表0和1
    m = []string{"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"}
    path, res = make([]byte, 0, len(digits)), make([]string, 0)

    if digits == "" {
        return res
    }
    backtracking(digits, 0) // 0代表digits从第0个值开始取
    return res
}

func backtracking(digits string, index int) {
    if len(path) == len(digits) {
        tmp := make([]byte, len(path))
        copy(tmp, path)
        res = append(res, string(tmp))
        return
    }

    digit := digits[index] - '0'	// 转换为0-9
    str := m[digit]

    for i := 0; i < len(str); i++ {
        path = append(path, str[i])
        backtracking(digits, index+1)
        path = path[:len(path)-1]
    }
}
  • 时间复杂度: O(3^m * 4^n)，其中 m 是对应四个字母的数字个数，n 是对应三个字母的数字个数
  • 空间复杂度: O(3^m * 4^n)

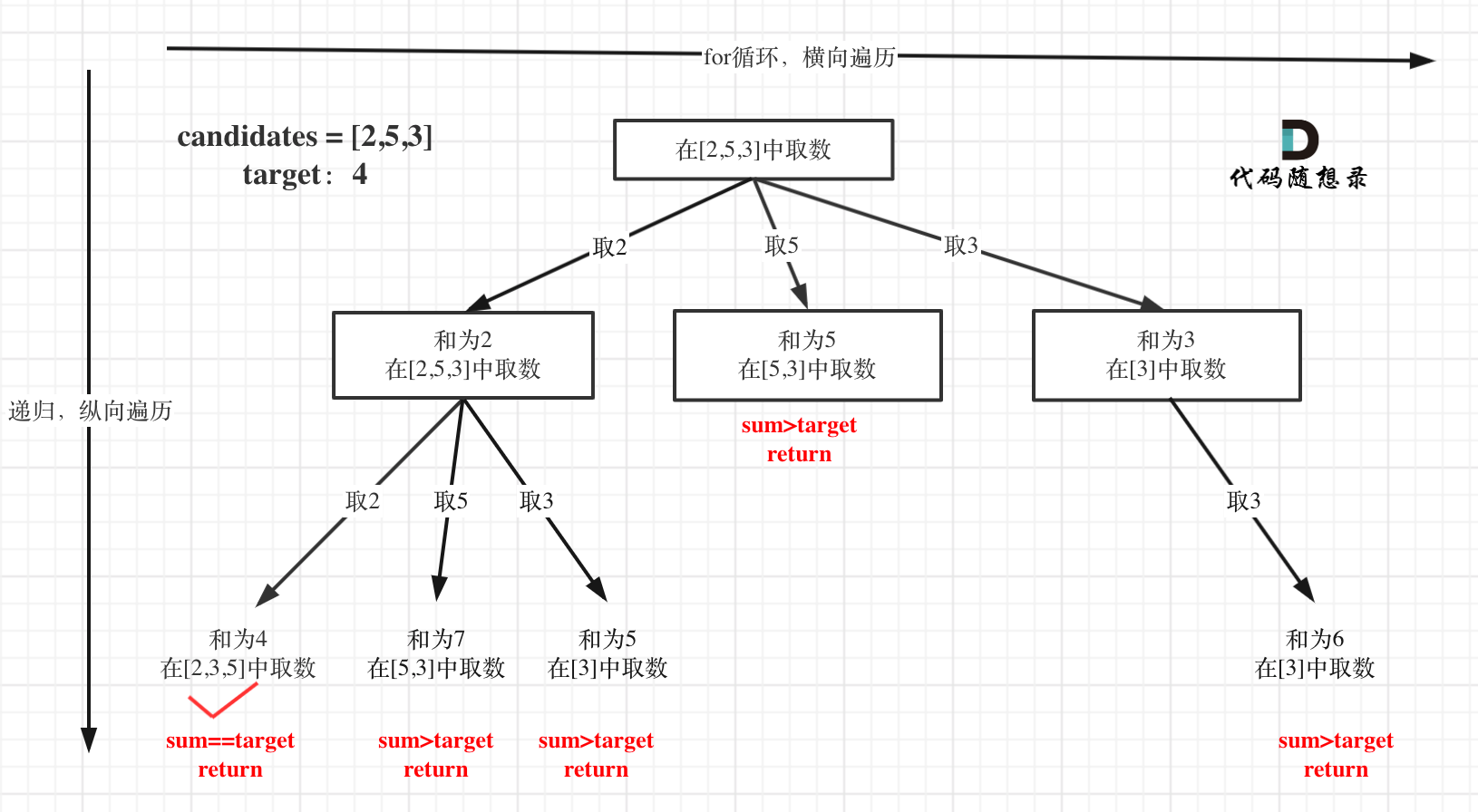
一个集合中的元素可以无限重复选取，但是有总和的限制。（横向遍历不能重复取，需要startIndex，但是纵向遍历可以重复读取当前的数，所以递归的时候传参i）

组合总和

Leetcode：39.组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

  • 所有数字（包括 target）都是正整数。
  • 解集不能包含重复的组合。

示例 1：

  • 输入：candidates = [2,3,6,7], target = 7,
  • 所求解集为： [ [7], [2,2,3] ]

示例 2：

  • 输入：candidates = [2,3,5], target = 8,
  • 所求解集为： [ [2,2,2,2], [2,3,3], [3,5] ]

思路分析：与前面组合问题一样，唯一不同的地方在于集合中的数字可以无限制重复被选取，也就是纵向遍历可以重复选取，横向遍历不能重复选取（如果横向遍历重复选取，会出现重复的组合），所以需要用到startIndex，但是递归传参时传递的不是i+1，而是i，传递i，代表可以重复选择集合中的元素；其次，在求和问题中，排序之后加剪枝是常见的套路！，所以还需要在递归前进行排序。

回溯算法组合问题2示意图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
var ( 
    path []int
    res [][]int
)

func combinationSum(candidates []int, target int) [][]int {
    path, res = make([]int, 0, len(candidates)), make([][]int, 0)
    sort.Ints(candidates)   // 排序，为剪枝做准备
    backtracking(candidates, 0, target, 0)
    return res
}

func backtracking(candidates []int, sum, target int, startIndex int) {
    if sum > target {   // 剪枝
        return
    }
    if sum == target {
        tmp := make([]int, len(path))
        copy(tmp, path)
        res = append(res, tmp)
        return
    }

    for i := startIndex; i < len(candidates); i++ {
        path = append(path, candidates[i])
        sum += candidates[i]
        backtracking(candidates, sum, target, i)    // 不用i+1了，表示可以重复读取当前的数
        path = path[:len(path)-1]
        sum -= candidates[i]
    }
}

  • 时间复杂度: O(n * 2^n)，注意这只是复杂度的上界，因为剪枝的存在，真实的时间复杂度远小于此
  • 空间复杂度: O(target)

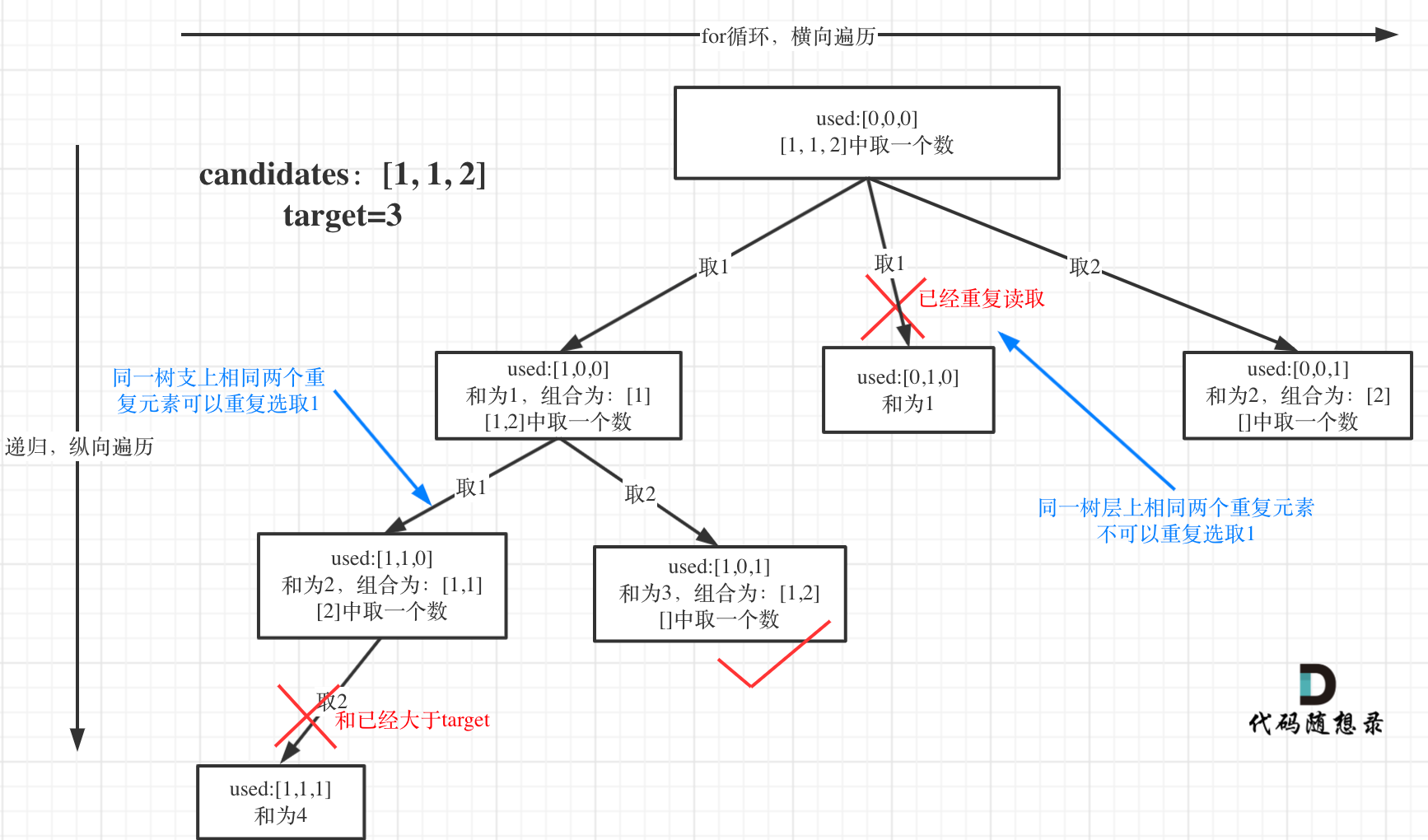
一个集合中的元素只能使用一次，并且数组是有重复的元。（需要startIndex，并且要先排序数组，然后进行剪枝）

组合总和 II

Leetcode：40.组合总和 II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。

注意：解集不能包含重复的组合。

示例 1:

1
2
3
4
5
6
7
8
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

思路：本类型题目与前面题目区别在于集合（数组candidates）有重复元素，但还不能有重复的组合。所以在此基础上，需要对集合进行去重，也就是对树结构中同一层进行去重，去重前首先要排序，保证集合是有序的。

回溯算法组合去重示意图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
var ( 
    path []int
    res [][]int
)

func combinationSum2(candidates []int, target int) [][]int {
    path, res = make([]int, 0, len(candidates)), make([][]int, 0)
    sort.Ints(candidates)   // 排序，为剪枝和去重做准备
    backtracking(candidates, 0, target, 0)
    return res
}

func backtracking(candidates []int, sum, target int, startIndex int) {
    if sum > target {   // 剪枝
        return
    }
    if sum == target {
        tmp := make([]int, len(path))
        copy(tmp, path)
        res = append(res, tmp)
        return
    }

    for i := startIndex; i < len(candidates); i++ {
        // 去重，如果前一个数与后一个数相同，则两个分支必定相同
        if i > startIndex && candidates[i] == candidates[i-1] {
            continue
        }
        path = append(path, candidates[i])
        sum += candidates[i]
        backtracking(candidates, sum, target, i+1)    // 用i+1，表示不可以重复读取当前的数
        path = path[:len(path)-1]
        sum -= candidates[i]
    }
}
  • 时间复杂度: O(n * 2^n)
  • 空间复杂度: O(n)

切割问题

其实切割问题类似组合问题。

例如对于字符串abcdef：

  • 组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中再选取第三个…..。
  • 切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中再切割第三段…..。

分割回文串

Leetcode：131.分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例 1：

1
2
输入：s = "aab"
输出：[["a","a","b"],["aa","b"]]

示例 2：

1
2
输入：s = "a"
输出：[["a"]]

列出如下几个难点：

  • 切割问题其实类似组合问题

  • 如何模拟那些切割线 ——————递归参数需要传入startIndex，表示下一轮递归遍历的起始位置，这个startIndex就是切割线

  • 切割问题中递归如何终止 ——————当切割线index达到数组最后，递归就终止

  • 在递归循环中如何截取子串

  • 如何判断回文

回溯算法判断是否回文串示意图

思路：关于模拟切割线，其实就是startIndex是上一层已经确定了的分割线，i是这一层试图寻找的新分割线

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
var (
    path []string
    res [][]string
)

func partition(s string) [][]string {
    path, res = make([]string, 0, len(s)), make([][]string, 0)
    backtracking(s, 0)
    return res
}

func backtracking(s string, startIndex int) {
    // 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了
    if startIndex >= len(s) {
        tmp := make([]string, len(path))
        copy(tmp, path)
        res = append(res, tmp)
        return
    }

    for i := startIndex; i < len(s); i++ {
        str := s[startIndex:i+1]    // 切割出来当前需要处理的字符
        if isPalindrome(str) {   // 是回文子串，才继续往下走
            path = append(path, str)
            backtracking(s, i+1)        // 寻找i+1为起始位置的子串
            path = path[:len(path)-1]   // 回溯过程，弹出本次已经添加的子串
        }
    }
}

func isPalindrome(s string) bool {
    for i, j := 0, len(s)-1; i < j; i, j = i+1, j-1 {
        if s[i] != s[j] {
            return false
        }
    }
    return true
}
  • 时间复杂度: O(n * 2^n)
  • 空间复杂度: O(n^2)

子集问题

在树形结构中子集问题是要收集所有节点的结果，而组合问题、分割问题是收集叶子节点的结果，所以一般来说递归不用加终止条件，让for循环遍历完整棵树，然后终止。

不需要去重，收集树中每个节点的值

子集

Leetcode：78.子集

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例: 输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]

思路：收集每一个节点的值，所以没有返回条件

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
var ( 
    path []int
    res [][]int
)

func subsets(nums []int) [][]int {
    path, res = make([]int, 0, len(nums)), make([][]int, 0)
    backtracking(nums, 0)
    return res
}

func backtracking(nums []int, startIndex int) {
    // 收集每一个节点的值，所以没有返回条件，不需要return
    tmp := make([]int, len(path))
    copy(tmp, path)
    res = append(res, tmp)

    for i := startIndex; i < len(nums); i++ {
        path = append(path, nums[i])
        backtracking(nums, i+1) // 不能重复取值，所以传i+1
        path = path[:len(path)-1]
    }
}
  • 时间复杂度: O(n * 2^n)
  • 空间复杂度: O(n)

需要去重， 先排序再去重剪枝

类似组合问题中的去重，先排序数组，然后进行剪枝，即当前元素与前一个元素相同，则当前元素的分支比与前一个元素分支相同。

子集II

Leetcode：90.子集II

给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

  • 输入: [1,2,2]
  • 输出: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]

思路：增加去重逻辑

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
var ( 
    path []int
    res [][]int
)

func subsetsWithDup(nums []int) [][]int {
    path, res = make([]int, 0, len(nums)), make([][]int, 0)
    sort.Ints(nums)   // 排序，为剪枝和去重做准备
    backtracking(nums, 0)
    return res
}

func backtracking(nums []int, startIndex int) {
    // 收集每一个节点的值，所以没有返回条件
    tmp := make([]int, len(path))
    copy(tmp, path)
    res = append(res, tmp)

    for i := startIndex; i < len(nums); i++ {
        // 去重，如果前一个数与后一个数相同，则两个分支必定相同
        if i > startIndex && nums[i] == nums[i-1] {
            continue
        }
        path = append(path, nums[i])
        backtracking(nums, i+1) // 不能重复取值，所以传i+1
        path = path[:len(path)-1]
    }
}
  • 时间复杂度: O(n * 2^n)
  • 空间复杂度: O(n)

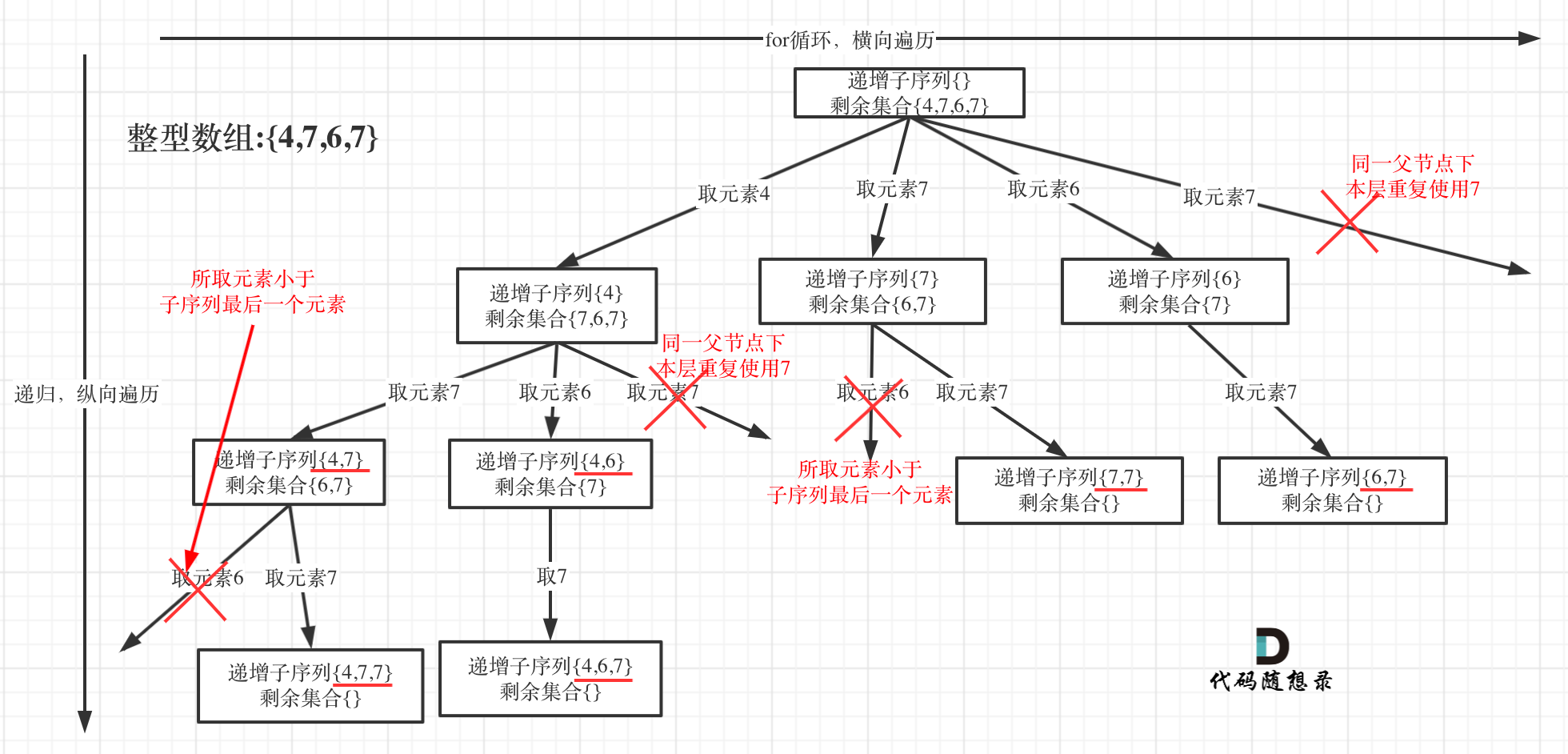
自增子序列，去重，求子集

递增子序列

Leetcode：491.递增子序列

给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。

示例:

输入: [4, 6, 7, 7] 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

说明:

给定数组的长度不会超过15。

数组中的整数范围是 [-100,100]。

给定数组中可能包含重复数字，相等的数字应该被视为递增的一种情况。

思路：该题由于是求集合中的递增子序列，所以不能用对原集合先排序后去重的方法，所以去重逻辑不仅仅是与本层中前一个节点进行对比去重，而是要与同一个父节点下本层中所有之前的节点进行对比去重，用哈希表set进行去重。

回溯算法递增子序列流程图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
var ( 
    path []int
    res [][]int
)

func findSubsequences(nums []int) [][]int {
    path, res = make([]int, 0, len(nums)), make([][]int, 0)
    backtracking(nums, 0)
    return res
}

func backtracking(nums []int, startIndex int) {
    // 收集每一个节点的值
    if len(path) > 1 {
        tmp := make([]int, len(path))
        copy(tmp, path)
        res = append(res, tmp)
        // 注意这里不要加return，要取树上的节点
    }

    set := make(map[int]struct{}, 0)    // 用set对本层元素进行去重，每一层都有一个新的set
    for i := startIndex; i < len(nums); i++ {
        // 去重，如果当前值在本层出现过，则两个分支必定相同
        if _, ok := set[nums[i]]; ok {
            continue
        }

        // 判断是否是递增元素
        if len(path) == 0 || nums[i] >= path[len(path)-1] {
            set[nums[i]] = struct{}{}
            path = append(path, nums[i])
            backtracking(nums, i+1) // 不能重复取值，所以传i+1
            path = path[:len(path)-1]
        }
    }
}
  • 时间复杂度: O(n * 2^n)
  • 空间复杂度: O(n)

排列问题

  • 每层都是从0开始搜索而不是startIndex

  • 需要used数组记录path里都放了哪些元素了

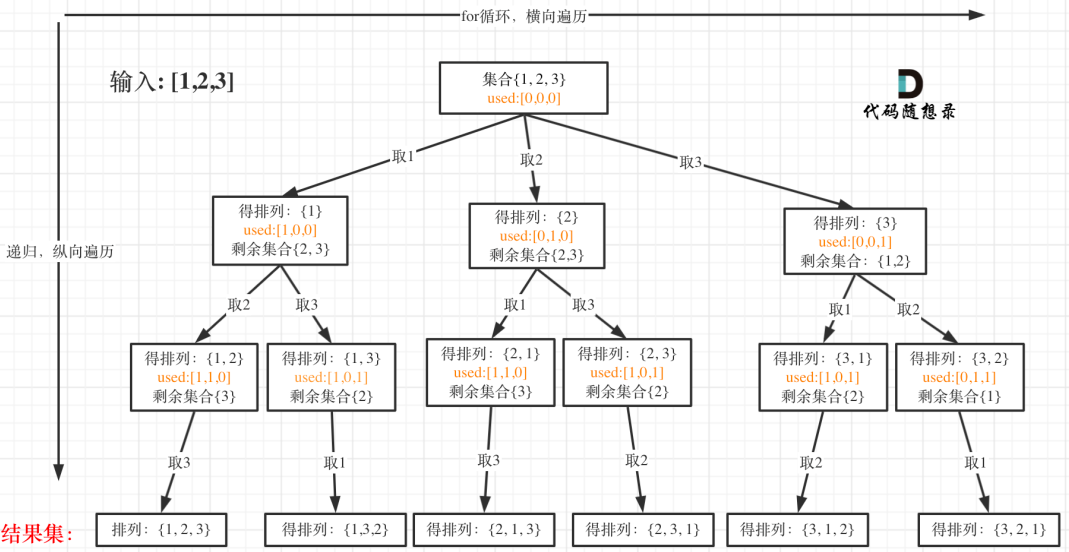
不需要去重

全排列

Leetcode：46.全排列

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

  • 输入: [1,2,3]
  • 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

思路：排列问题，每次都要从头开始搜索，所以不需要startIndex，而used数组，其实就是记录此时path里都有哪些元素使用了（记录元素位置），一个排列里一个元素只能使用一次（正是由于每次都要从头开始搜索集合，所以才需要used数组）。

回溯算法不需要去重全排列示意图

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
var ( 
    path []int
    res [][]int
)

func permute(nums []int) [][]int {
    path, res = make([]int, 0, len(nums)), make([][]int, 0)
    used := make(map[int]struct{}, 0)
    backtracking(nums, used)
    return res
}

func backtracking(nums []int, used map[int]struct{}) {
    if len(nums) == len(path) {
        tmp := make([]int, len(path))
        copy(tmp, path)
        res = append(res, tmp)
        return
    }

    for i := 0; i < len(nums); i++ {
        // 由于每次遍历都是从头开始，所以需要去掉已使用过的元素
        if _, ok := used[i]; ok {
            continue
        }
        used[i] = struct{}{}  // 记录已使用的元素的位置
        path = append(path, nums[i])

        backtracking(nums, used)

        delete(used, i)
        path = path[:len(path)-1]
    }
}
  • 时间复杂度: O(n!)
  • 空间复杂度: O(n)

需要去重

全排列 II

Leetcode：47.全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

1
2
3
4
5
输入：nums = [1,1,2]
输出：
[[1,1,2],
 [1,2,1],
 [2,1,1]]

示例 2：

1
2
输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

  • 1 <= nums.length <= 8
  • -10 <= nums[i] <= 10

思路：需要先对集合进行排序，判断当前的值是否使用过，再对同一个层相同的两个分支进行去重。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

var ( 
    path []int
    res [][]int
)

func permuteUnique(nums []int) [][]int {
    path, res = make([]int, 0, len(nums)), make([][]int, 0)
    used := make(map[int]struct{}, 0)
    sort.Ints(nums)
    backtracking(nums, used)
    return res
}

func backtracking(nums []int, used map[int]struct{}) {
    if len(nums) == len(path) {
        tmp := make([]int, len(path))
        copy(tmp, path)
        res = append(res, tmp)
        return
    }

    for i := 0; i < len(nums); i++ {
        // 由于每次遍历都是从头开始，所以需要去掉已使用过的元素；判断当前的值是否使用过
        if _, ok := used[i]; ok {
            continue
        }

        // i-1的元素已经使用过了，并且当前i元素的值与i-1元素的值相同，则两个分支必然相同
        if _, ok := used[i-1]; ok && i > 0 && nums[i] == nums[i - 1]{
            continue
        }

        used[i] = struct{}{}  // 记录已使用的元素
        path = append(path, nums[i])

        backtracking(nums, used)

        delete(used, i)
        path = path[:len(path)-1]
    }
}
  • 时间复杂度: O(n! * n)
  • 空间复杂度: O(n)